今天读文献读到一个计算出租车距离计算,
Driving distances are approximated by multiplying the Euclidean distance between origin and destination by a factor of α = 1.4, to reflect the “taxicab geometry” of typical driving grids; since the greatest possible upscale is α = √2 —which would reflect the diagonal of a square with available roads only on a right-angled grid pattern—the proportionality factor of 1.4 represents an upper bound.
曼哈顿距离 (Manhattan Distance) 也叫做计程车几何(Taxicab geometry),也就是欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。下图A到B直线就是欧式距离,紫色线就是曼哈顿距离。如下图所示:
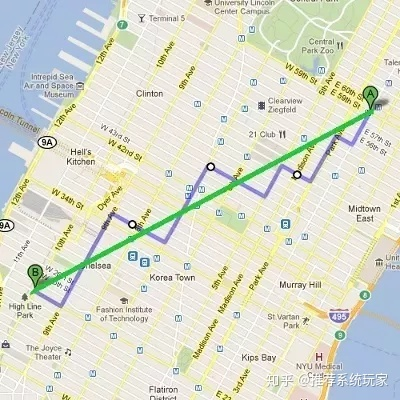
但是实际道路可能并不如上图都是直角转弯,也可能有弯曲的地方,那样子路线长度就比曼哈顿距离短,所以存在上文引用中所写的:the proportionality factor of 1.4 represents an upper bound.
Reference
Kang N, Feinberg F M, Papalambros P Y. Autonomous electric vehicle sharing system design[J]. Journal of Mechanical Design, 2017, 139(1).